This is post #3 of my Vector Angle series. Make sure you check out the first post for a quick introduction!

Method #3: Projection⌗

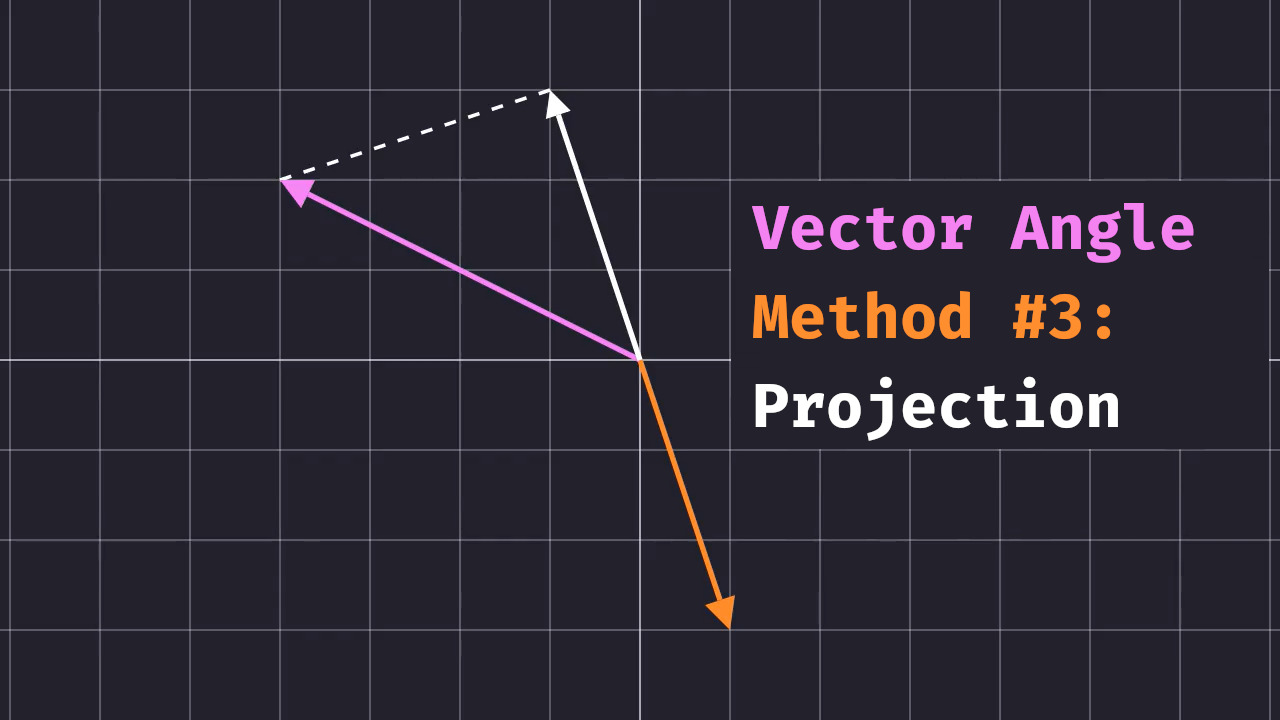
Projection is a cool topic. Explained visually, we’re finding the best approximation for the purple vector, if it had to be on the same line as the orange vector. It’s the closest approximation for a vector constrainted to a given subspace.

If you don’t quite get it yet, don’t worry, we’ll build up some intuition before we dive into the math.

Projection is useful because it allows us to use one of its cool properties. Any vector, when projected onto a line, plane, or n-1 dimensional space is guaranteed¹ to form a right angle with the line/plane/whatever.

Once we compute the projection, we will have two pieces of information. Two sides of a triangle with an identical $\theta$, but now with angle $A$ guaranteed to be 90 deg.

That sounds good, but before we go any further, let’s build an intuition for what projection does.

Building Intuition⌗

When we’re projecting one vector onto another vector, visualize that we’re projecting the vector’s tip (the point) onto another vector’s subspace (the line). A subspace is basically any point that we can reach by scaling a vector by a constant.

The shortest line from a point to a subspace (line) forms a perpendicular angle with the subspace.

This is helpful since a projection is exactly that - the projected point has the shortest possible distance from the subspace to the original point.

We can also reason about the process by looking at the unit vectors of the space.

When we project one unit vector onto this subspace, we calculate the length of the projected vector. Remember, the projection is the closest we can get from the tip of the green vector (the point) to the subspace defined by the pink vector (the line).

Next, we calculate the length for the projection of the other unit vector.

Now, when projecting a vector onto that subspace, we can just split it into unit vectors, and multiply it by the projection multiples (1.2x and 0.98x).

A simple way of thinking about this is that we want the projected vector to reside on the pink vector’s line. To do that, we want to multiply the pink vector by a constant so that it is the closest it can get to the purple vector without leaving the pink vector’s subspace.

With the process above, we’re getting the closest we can for each component of the vector and adding those components together to calculate the answer.

(P.S. If you understand what we’re doing there, try combining that with your understanding of matricies as linear transformations. You can really understand what projection matricies are doing!²)

Now let’s use this right angle in our calculations!

Practical Application⌗

Let’s do it

Given two vectors $a$ and $b$, let’s project vector b onto the subspace defined by vector $a$.

Here’s the formula for the projection of vector $b$ onto vector $a$:

$$ b_{proj} = \frac{a \cdot b}{|a|^2} a = \frac{a \cdot b}{a \cdot a} a $$

Now we have a way to get the three sides that we need, and we can choose which sides to use in our calculation.

Side A length formula:

$|v|$

Side B length formula:

$|\frac{u \cdot v}{u \cdot u}u|$

Side C length formula:

$|v - \frac{u \cdot v}{u \cdot u}u|$

Now we could technically choose any of these 2 lengths, so let’s try all 3 possibilities and see which one is simplest.

Sin $\frac{Opp}{Hyp}$

$$\frac{|v - \frac{u \cdot v}{u \cdot u}u|}{|v|}$$

$$\frac{\sqrt{{(v - \frac{u \cdot v}{u \cdot u}u)}^2}}{\sqrt{(v)^2}}$$

$$\sqrt{\frac{{(v - \frac{u \cdot v}{u \cdot u}u)}^2}{v^2}}$$

$$\sqrt{\frac{{v^2 - 2(v\frac{u \cdot v}{u \cdot u}u)} + (\frac{u \cdot v}{u \cdot u}u)^2}{v^2}}$$

Cos $\frac{Adj}{Hyp}$

$$\frac{|\frac{u \cdot v}{u \cdot u}u|}{|v|}$$

$$\frac{\sqrt{(\frac{u \cdot v}{u \cdot u}u)^2}}{\sqrt{v^2}}$$

$$\sqrt{\frac{(\frac{u \cdot v}{u \cdot u}u)^2}{v^2}}$$

Tan $\frac{Opp}{Adj}$

$$\frac{|v - \frac{u \cdot v}{u \cdot u}u|}{|\frac{u \cdot v}{u \cdot u}u|}$$

$$\frac{\sqrt{(v - \frac{u \cdot v}{u \cdot u}u)^2}}{\sqrt{(\frac{u \cdot v}{u \cdot u}u)^2}}$$

$$\sqrt{\frac{(v - \frac{u \cdot v}{u \cdot u}u)^2}{(\frac{u \cdot v}{u \cdot u}u)^2}}$$

$$\sqrt{\frac{{v^2 - 2(v\frac{u \cdot v}{u \cdot u}u)} + (\frac{u \cdot v}{u \cdot u}u)^2}{(\frac{u \cdot v}{u \cdot u}u)^2}}$$

Simplify⌗

Alright, so now we know that the simplest option is to use Cos because it is the only option that exclusively uses the adjacent and hypotenuse sides. When using projection, we can only calculate the opposite side after we know the hypotenuse and adjacent sides, so it makes sense to use those sides directly.

$$\text{angle} = \arccos{\bigg(\sqrt{\frac{(\frac{u \cdot v}{u \cdot u}u)^2}{v \cdot v}}\bigg)}$$

This is the simplest that we can make the equation - it’s our final answer!

Wait a second…⌗

We spotted a problem in our last blog post regarding obtuse angles. That also happens with this method.

Since the projection can face the opposite direction of the initial line, our $\theta$ will always be acute. We can detect and fix this by calculating if $b$ and $b_{proj}$ face the same way. If they aren’t, then the actual angle is $180 - \theta$.

<- Up Next⌗

We just derived an alternative way to use the dot product to calculate the angle between two vectors - using projection as a starting point!

We’ve now covered 3 different methods of calculating the angle formed by two vectors:

1. Standard (Law of Cosines)
2. Visual (Change of Basis)
3. Alternative (Projection)

Up next, we’re going to benchmark these different methods and see which one is fastest on a computer.

<- Read the next post Previous ->