This is the final post (#4) of my Vector Angle series. Make sure you check out the first post for a quick introduction!

So far we’ve covered 3 methods for calculating the angle formed by 2 vectors.

1. Standard (Law of Cosines)
2. Visual (Change of Basis)
3. Alternative (Projection)

Unfortunately, since we didn’t derive a general formula for the change of basis calculations, I’m going to exclude it from this benchmarking process.

Analysis⌗

Before we write any code, let’s analyze the equations themselves.

Law of Cosines (w/ explicit magnitude calculations) $$ \theta = \arccos {\bigg(\frac {v \cdot u}{{\sqrt{v\cdot v}}{\sqrt{u\cdot u}}}\bigg)} $$

Projection $$\theta = \arccos{\bigg(\sqrt{\frac{(\frac{u \cdot v}{u \cdot u}u)^2}{v \cdot v}}\bigg)}$$

We can make the projection method better for computers by rearranging some terms: $$ = \arccos{\bigg(\sqrt{\frac{(\frac{u \cdot v}{u \cdot u})^2(u\cdot u)}{v \cdot v}}\bigg)}$$ $$ = \arccos{\bigg(\sqrt{\frac{\frac{(u \cdot v)^2}{u \cdot u}}{v \cdot v}}\bigg)}$$ $$ = \arccos{\bigg(\sqrt{\frac{(u \cdot v)^2}{(v \cdot v)(u \cdot u)}}\bigg)}$$

Ops	Law of Cosines	Projection
Dot product	3	3
Division	1	1
Constant * Constant	1	2
Sqrt	2	1
Arccos	1	1

Now let’s do this table again, but put it in terms of the input vector’s dimensions ($n$).

• Dot products are $n$ multiplication and $n-1$ additions.

Ops	Law of Cosines	Projection
Addition	3n - 1	3n - 1
Multiplication	3n + 1	3n + 2
Division	1	1
Sqrt	2	1
Arccos	1	1

From this table, it looks like it’ll be a close fight. The only difference is between the number of multiplications and sqrt operations.

Wait a second…⌗

If we look at the re-arranged Projection method: $$\theta = \arccos{\bigg(\sqrt{\frac{(u \cdot v)^2}{(v \cdot v) (u \cdot u)}}\bigg)}$$

and compare it to the Law of Cosines method: $$ \theta = \arccos {\bigg(\frac {v \cdot u}{{\sqrt{v\cdot v}}{\sqrt{u\cdot u}}}\bigg)} $$

There’s something eerily similar about the two equations.

What if we take the Law of Cosines method, square it, then take the square root? $$ = \arccos {\bigg(\sqrt{\bigg(\frac {v \cdot u}{{\sqrt{v\cdot v}}{\sqrt{u\cdot u}}}\bigg)^2} \text{ } \bigg)} $$ $$ = \arccos {\bigg(\sqrt{\frac {(v \cdot u)^2}{{(\sqrt{v\cdot v}}{\sqrt{u\cdot u})^2}}} \text{ } \bigg)} $$ $$ = \arccos {\bigg(\sqrt{\frac {(v \cdot u)^2}{{(v\cdot v)}{(u\cdot u)}}} \text{ } \bigg)} $$

Woah.

I wasn’t expecting that.

Both independently derived methods are the same.

The only difference is that the Projection method always provides a positive value to $arccos$, which is the reason why we only get acute angles from that method.

I had planned to dive into some of the assembly code and have a bunch of performance charts, but I guess that isn’t needed now.

Why use the Law of Cosines method?⌗

Computers don’t use the alternative arrangement provided by the projection method. One of the main reasons¹ for this is that computers provide a fast reciprocal sqrt op that is faster than a normal sqrt op.

That changes the table above:

Ops	Law of Cosines	Projection
Addition	3n - 1	3n - 1
Multiplication	3n + 1->3n + 2	3n + 2
Division	1->0	1
Sqrt	2->0	1
1/Sqrt	0->2	0
Arccos	1	1

Division and sqrt functions are expensive for computers, so the ability to eliminate all those ops makes a big difference.

Closing Thoughts⌗

Thanks for coming along with me on this ride, it was fun to take the time to solidify my understanding of these linear algebra concepts.

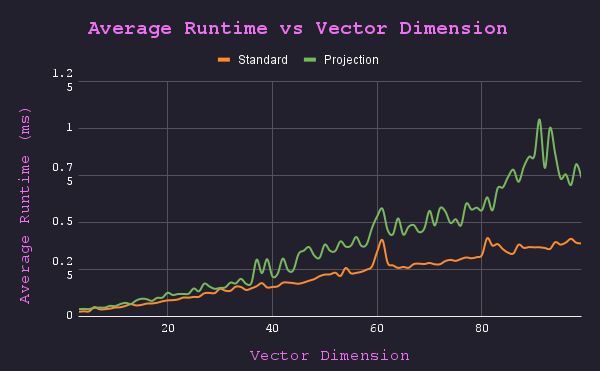
Strangely enough, the projection method performs better than the Law of Cosines method when it is run using CPython. When implemented with a compiled language like C++, the Law of Cosines method has a faster runtime (as expected).

Disclaimer: This code was written before I discovered the equivalence, so it relies on the compiler to simplify the projection method from this form: $$\theta = \arccos{\bigg(\sqrt{\frac{(\frac{u \cdot v}{u \cdot u}u)^2}{v \cdot v}}\bigg)}$$

Check out the benchmark code

Shoutout to @Qwendu for writing the C++ benchmarking code after I first posted about this on Reddit.

As always, feel free to try out the code on your own and make pull requests to improve it.

Previous ->